In this section we learn a theoretically important existence theorem called theIntermediate Value Theorem and we investigate some applications.
Solved: Apply the Intermediate Value Theorem to f(x) = 7x - cos 9x on 0, 1, evaluate f(0) and f(1). (Round your answers to two decimal places.). For Teachers for Schools for Working Scholars. X Exclude words from your search Put - in front of a word you want to leave out. For example, jaguar speed -car Search for an exact match Put a word or phrase inside quotes.
Intermediate Value Theorem
In this section we discuss an important theorem related to continuous functions.Before we present the theorem, lets consider two real life situations and observe animportant difference in their behavior. First, consider the ambient temperature andsecond, consider the amount of money in a bank account.
First, suppose that the temperature is at 8am and then suppose it is at noon.Because of the continuous nature of temperature variation, we can be surethat at some time between 8am and noon the temperature was exactly .Can we make a similar claim about money in a bank account? Supposethe account has $65 in it at 8am and then it has $75 in it at noon. Did ithave exactly $70 in it at some time between 8 am and noon? We cannotanswer that question with any certainty from the given information. On onehand, it is possible that a $10 deposit was made at 11am and so the total inthe bank would have jumped from $65 dollars to $75 without ever beingexactly $70. On the other hand, it is possible that the $10 was added in $5increments. In this case, the account did have exactly $70 in it at some time. Thefundamental reason why we can make certain conclusions in the first casebut cannot in the second, is that temperature varies continuously, whereasmoney in a bank account does not (it will have jump discontinuities). When aquantity is known to vary continuously, then if the quantity is observed to havedifferent values at different times then we can conclude that the quantitytook on any given value between these two at some time between our twoobservations. Mathematically, this property is stated in the Intermediate ValueTheorem.
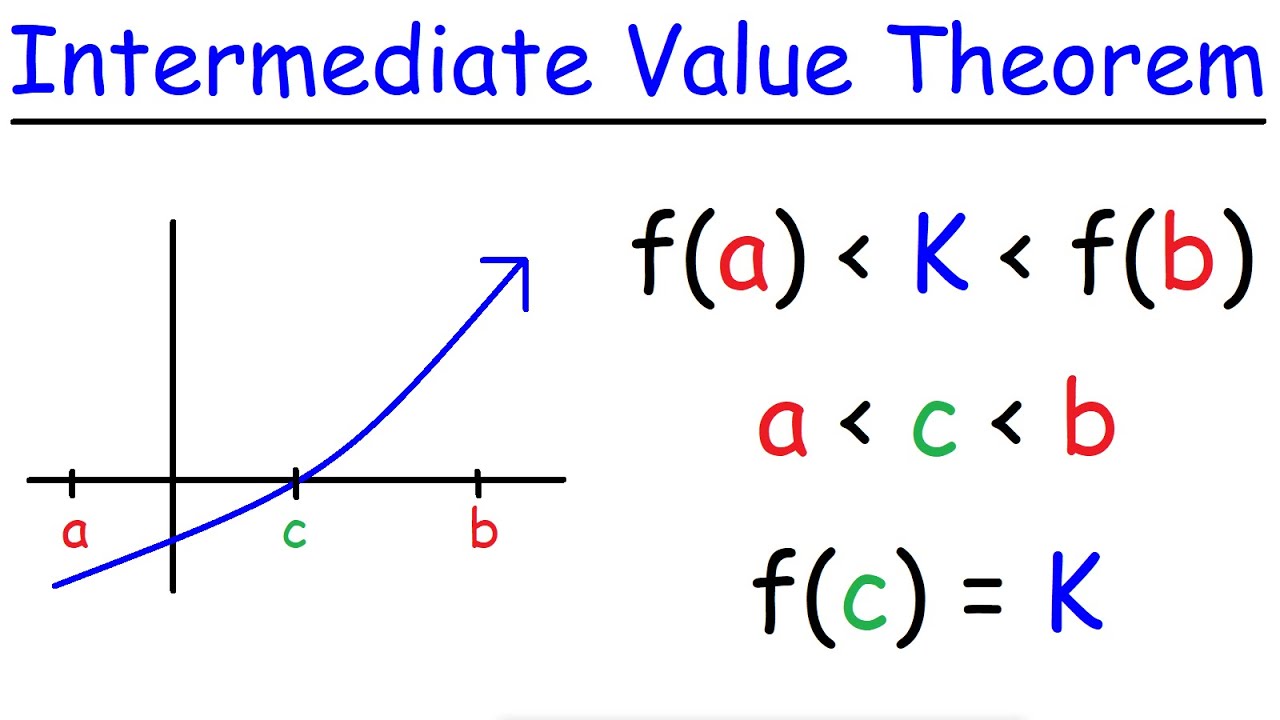
Intermediate Value TheoremIf the function is continuous on the closed interval and is a number between and ,then the equation has a solution in the open interval .
The value in the theorem is called an intermediate value for the function on theinterval . Note that if a function is not continuous on an interval, then the equation may or may not have a solution on the interval.
Remark: saying that has a solution in is equivalent to saying that there exists anumber between and such that .
The following figure illustrates the IVT.
First, the function is continuous on the interval since is a polynomial. Second,observe that and so that 10 is an intermediate value, i.e., Now we can apply theIntermediate Value Theorem to conclude that the equation has a least one solutionbetween and . In this example, the number 10 is playing the role of in the statementof the theorem.
Is continuous on the closed interval ?
and
Is an intermediate value?
Can we apply the IVT to conclude that the equation has a solution in the openinterval ?
example 2 Show that the equation has a solution between and .First, note that the function is continuous on the interval and hence it iscontinuous on the sub-interval, . Next, observe that and so that 2 is anintermediate value, i.e., Finally, by the Intermediate Value Theorem wecan conclude that the equation has a solution on the open interval . Inthis example, the number 2 is playing the role of in the statement of thetheorem.
(problem 2) Determine whether the IVT can be used to show that the equation has a solution in the open interval Is continuous on the closed interval ?1.7 Intermediate Value Theoremap Calculus 2nd Edition
and
Is an intermendiate value?
Does the IVT imply that the equation has a solution in the open interval ?
example 3 Show that the function has a root in the open interval .Recall that a root occurs when . Since is a polynomial, it is continuous on theinterval . Plugging in the endpoints shows that 0 is an intermediate value: and so By the IVT, we can conclude that the equation has a solution (and hence has aroot) on the open interval .
Intermediate Value Theorem Examples
(problem 3) Determine whether the IVT can be used to show that the function has aroot in the open interval .Is continuous on the closed interval ?
and
Is an intermendiate value?
Does the IVT imply that the function has a root in the open interval ?
Note that the equation is equivalent to the equation . The latter is the prefered formfor using the IVT. So let Since is the difference between two continuous functions, itis continuous on the closed interval . Next, we compute and and show that 0 is anintermediate value: and and so, By the IVT, the equation has a solution in theopen interval . Hence the equivalent equation has a solution on the sameinterval.
All textbook readings are from:
Apostol, Tom M. Calculus, Volume 1: One-Variable Calculus, with An Introduction to Linear Algebra. Waltham, Mass: Blaisdell, 1967. ISBN: 9780471000051.
Additional course notes by James Raymond Munkres, Professor of Mathematics, Emeritus, are also provided.
Mean Value Theorem
| SES # | TOPICS | TEXTBOOK READINGS | COURSE NOTES READINGS |
|---|---|---|---|
| Real numbers | |||
| 0 | Proof writing and set theory | I 2.1-2.4 | |
| 1 | Axioms for the real numbers | I 3.1-3.7 | |
| 2 | Integers, induction, sigma notation | I 4.1-4.6 | Course Notes A |
| 3 | Least upper bound, triangle inequality | I 3.8-3.10, I 4.8 | Course Notes B |
| 4 | Functions, area axioms | 1.2-1.10 | |
| The integral | |||
| 5 | Definition of the integral | 1.12-1.17 | |
| 6 | Properties of the integral, Riemann condition | Course Notes C | |
| 7 | Proofs of integral properties | 88-90, 113-114 | Course Notes D |
| 8 | Piecewise, monotonic functions | 1.20-1.21 | Course Notes E |
| Limits and continuity | |||
| 9 | Limits and continuity defined | 3.1-3.4 | Course Notes F |
| 10 | Proofs of limit theorems, continuity | 3.5-3.7 | |
| 11 | Hour exam I | ||
| 12 | Intermediate value theorem | 3.9-3.11 | |
| 13 | Inverse functions | 3.12-3.14 | Course Notes G |
| 14 | Extreme value theorem and uniform continuity | 3.16-3.18 | Course Notes H |
| Derivatives | |||
| 15 | Definition of the derivative | 4.3-4.4, 4.7-4.8 | |
| 16 | Composite and inverse functions | 4.10, 6.20 | Course Notes I |
| 17 | Mean value theorem, curve sketching | 4.13-4.18 | |
| 18 | Fundamental theorem of calculus | 5.1-5.3 | Course Notes K |
| 19 | Trigonometric functions | Course Notes L | |
| Elementary functions; integration techniques | |||
| 20 | Logs and exponentials | 6.3-6.7, 6.12-6.16 | Course Notes M |
| 21 | IBP and substitution | 5.7, 5.9 | Course Notes N |
| 22 | Inverse trig; trig substitution | 6.21 | |
| 23 | Hour exam II | ||
| 24 | Partial fractions | 6.23 | Course Notes N |
| Taylor's formula and limits | |||
| 25 | Taylor's formula | 7.1-7.2 | |
| 26 | Proof of Taylor's formula | Course Notes O | |
| 27 | L'Hopital's rule and infinite limits | 7.12-7.16 | Course Notes P |
| Infinite series | |||
| 28 | Sequences and series; geometric series | 10.1-10.6, 10.8 (first page only) | |
| 29 | Absolute convergence, integral test | 10.11, 10.13, 10.18 | |
| 30 | Tests: comparison, root, ratio | 10.12, 10.15 | Course Notes Q |
| 31 | Hour exam III | ||
| 32 | Alternating series; improper integrals | 10.17, 10.23 | |
| Series of functions | |||
| 33 | Sequences of functions, convergence | 11.1-11.2 | |
| 34 | Power series | 11.3-11.4 | Course Notes R |
| 35 | Properties of power series | Course Notes R | |
| 36 | Taylor series | 11.9 | Course Notes S |
| 37 | Fourier series | Course Notes T | |
Welcome!
This is one of over 2,400 courses on OCW. Explore materials for this course in the pages linked along the left.
MIT OpenCourseWare is a free & open publication of material from thousands of MIT courses, covering the entire MIT curriculum.
No enrollment or registration. Freely browse and use OCW materials at your own pace. There's no signup, and no start or end dates.

Knowledge is your reward. Use OCW to guide your own life-long learning, or to teach others. We don't offer credit or certification for using OCW.
Made for sharing. Download files for later. Send to friends and colleagues. Modify, remix, and reuse (just remember to cite OCW as the source.)
Extreme Value Theorem
Learn more at Get Started with MIT OpenCourseWare
